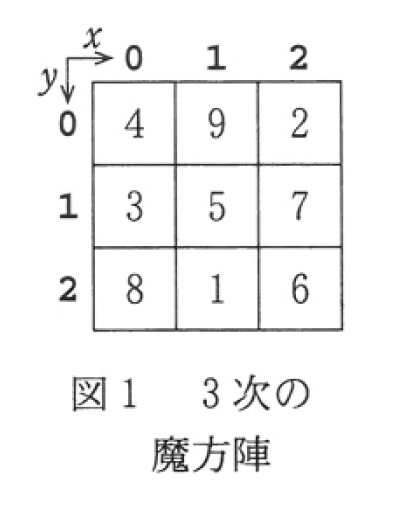
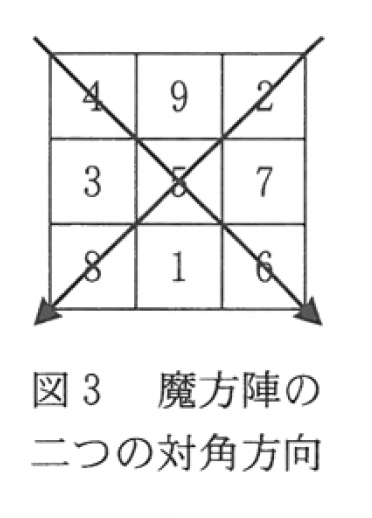
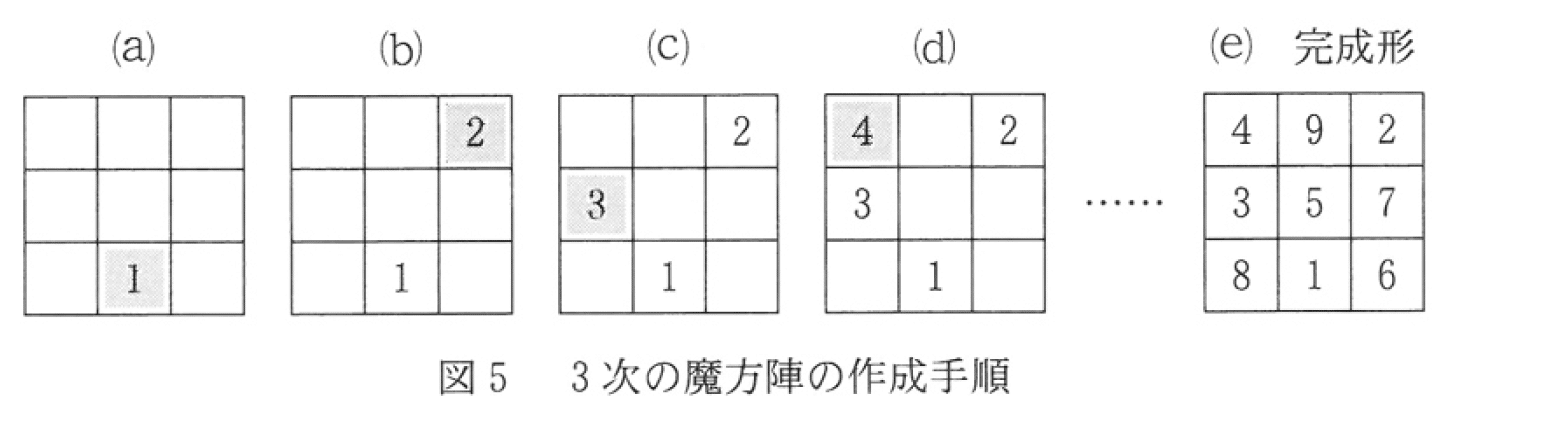
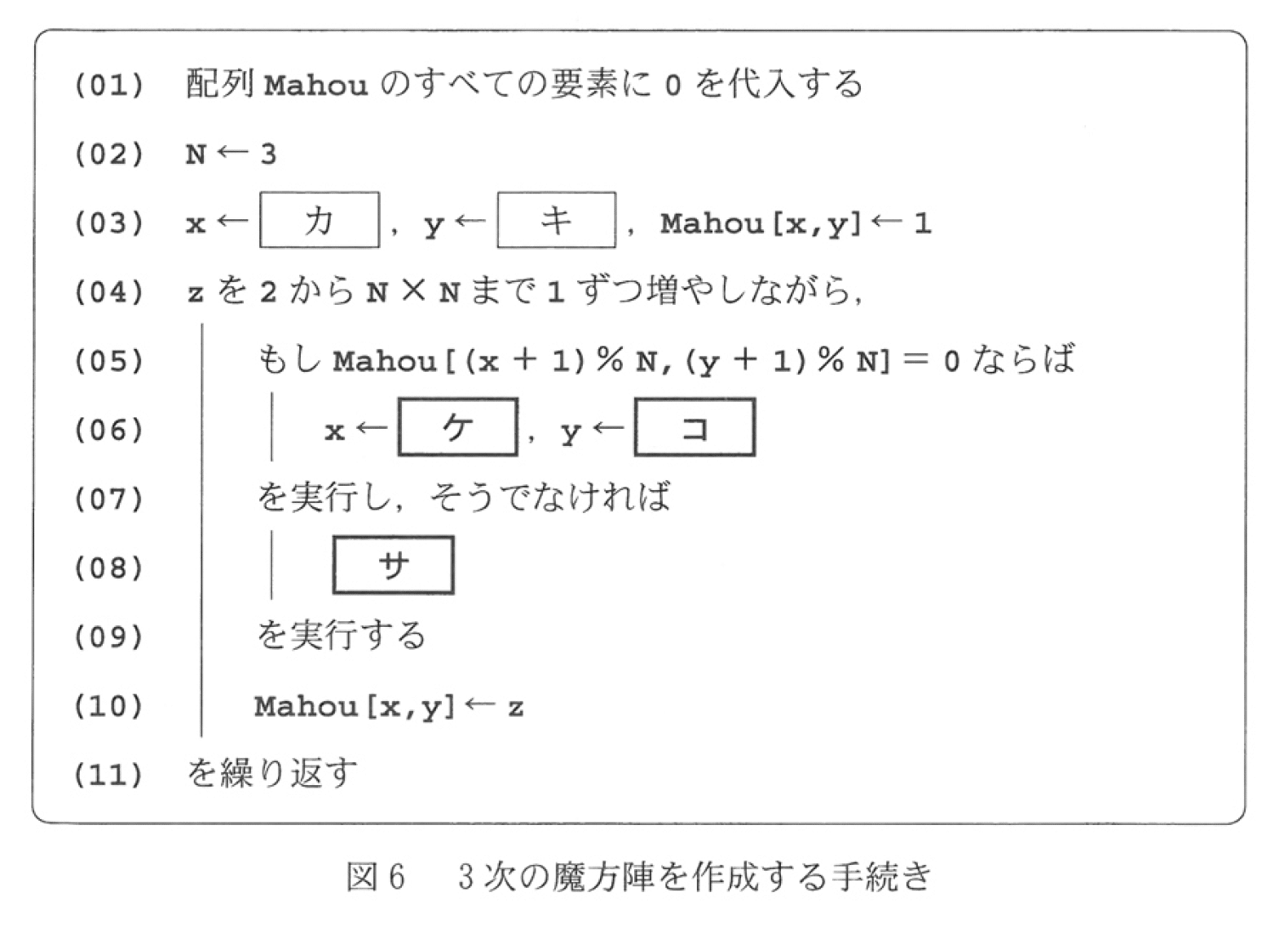
共通テスト「情報」最適化の原則 Vol.1　公開されているプログラム問題を見てみよう

 

「情報」では，「共通テスト対策」を謳った書籍，動画，コースなどのパッケージがあふれてきました．ただ「対策」という言葉に違和感を感じています．これからみんなで創っていく教科であり，質保証も十分でない黎明期に本当に重要なのは「対策」ではなく「最適化」していくことではないかと．そこで「最適化」と「原則」いう2つの単語を用いてアプローチしてみたいと思います．『共通テスト「情報」最適化の原則』という名称（略称ピクト）で連載していきたいと思います．なぜ略称がピクトかと言いますと，英語表記がPICTO ：Principles of Informatics of the Common Test Optimization　だからです．そもそもまだ共通テストも始まっておらず全体像が不明確で，「対策」とは如何にと思うのです．最適には，受験者がいかに最適化を駆使して限られた試験時間内で点数を取ることができるかという意味もあるのですが，情報の試験で問う問題ってどうあるべきかということを叡智を結集して最適化していこうという願いも込めています．

第1回目となる今回は，共通テスト教科「情報」のサンプル問題と試作問題2022のプログラミング問題を題材に，PICTO式でプログラム問題を解いてみたいと思います．

サンプル問題（令和3年3月24日公開）PICTO式で解いてみる．

2025年度入試(2025年1月)から教科「情報」が共通テストに追加されます．
すでに大学入試センターから令和3年3月24日にサンプル問題が出ています．

https://www.dnc.ac.jp/albums/abm.php?f=abm00040342.pdf&n=12_%E3%82%B5%E3%83%B3%E3%83%97%E3%83%AB%E5%95%8F%E9%A1%8C%E3%80%8E%E6%83%85%E5%A0%B1%E3%80%8F%E3%80%80%E5%95%8F%E9%A1%8C.pdf

まずはこのサンプル問題を見ていきましょう．
この第2問（7ページから12ページ）がプログラミング，アルゴリズムの問題です．この問題を実際に解いてみたいと思います．

以下，画像引用は上記PDF からの引用になります．

設問1

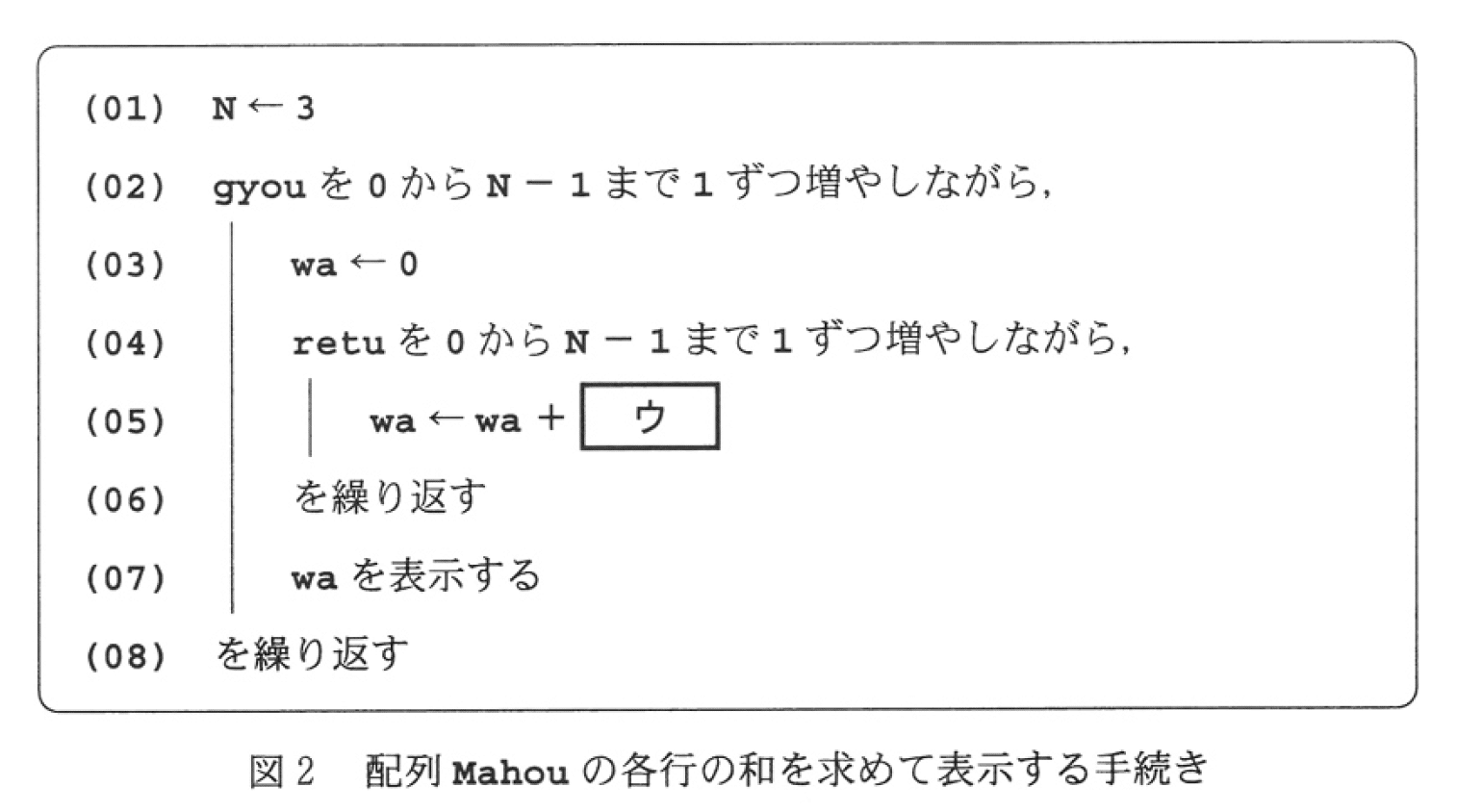
　まずいきなりですが，図3から見てみましょう．え！いきなりプログラムと解答群から見るんですか？と驚かれるかもしれませんが，とりあえず見てみましょう．

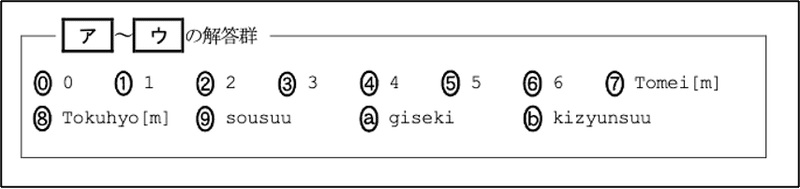
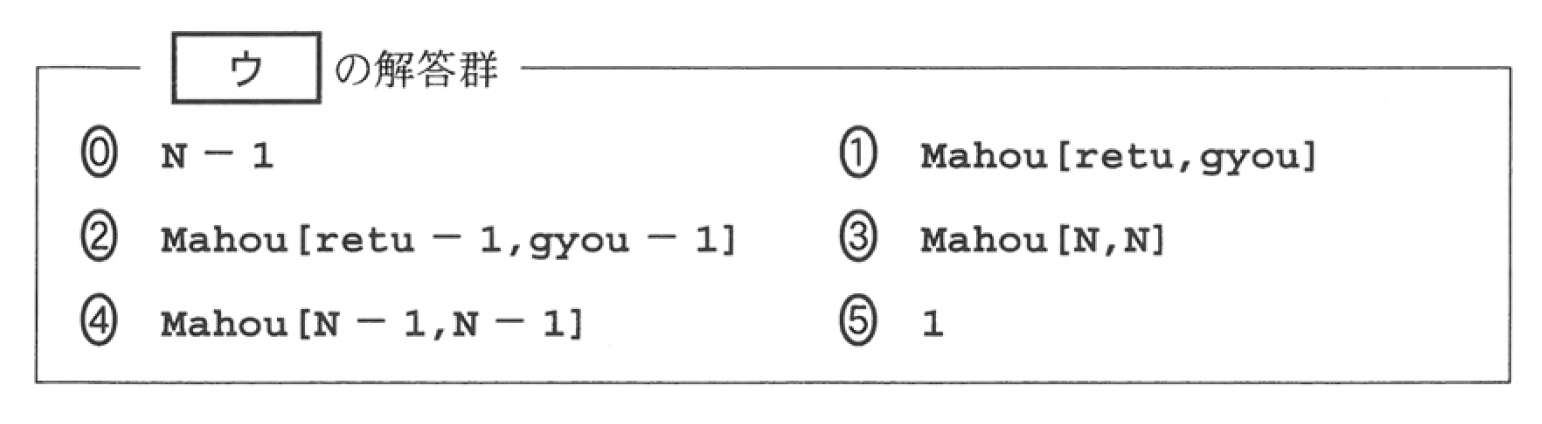
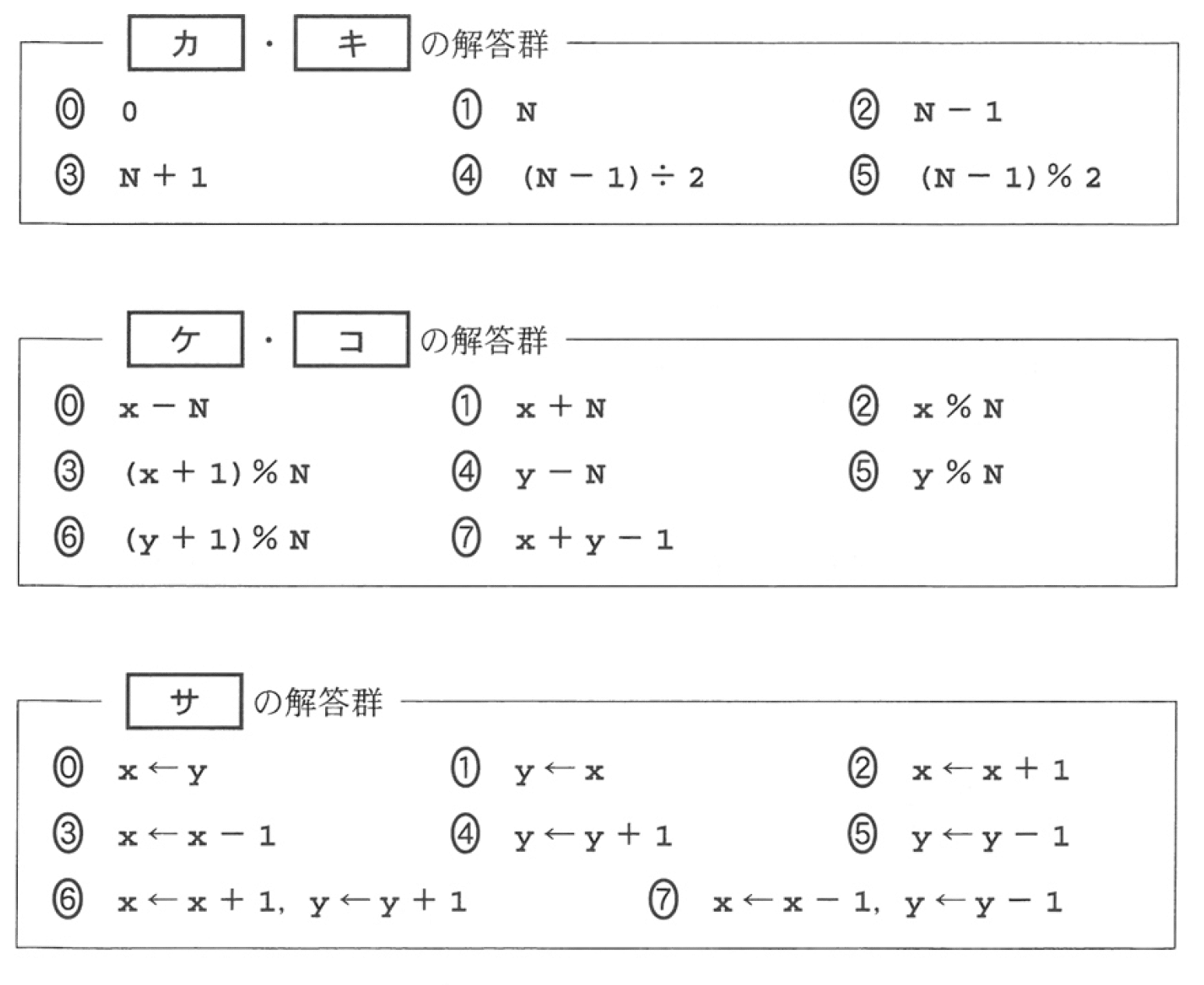
行(05),(06)を見ると，配列Tokuhyoの総計をsousuuに格納する処理であることが推測できます．配列の要素番号が0から始まるので，よって，[ア] は (配列Tokuhyoの要素数　- 1)と考えられます．ただし，選択肢にそのような記述はありません．また[m]が含まれている選択肢は，繰返しの回数が不定になります．DNCL2は擬似言語です．つまり挙動が分からないので，これは不適です． sousuuとgisekiの値は， 1回目に行05が実行される段階でそれぞれ0と6なので別解（(0),(6)）が存在してしまいます．またkizyunsuuはこの段階で初期化されていません．よって正答は，配列「得票」の要素数マイナス1をリテラルで表した(3)3 となります．

配列Tokuhyoの要素数が変わると正しく動作しなくなるのであまり良い例ではありませんが，試験という視点から考えると最初の空欄となりますので正答率が高くなるようにと思ったのだと考えられます．ただこれは，慣れている人にとっては逆に初見「正答がない」と思ってしまうかもしれません．
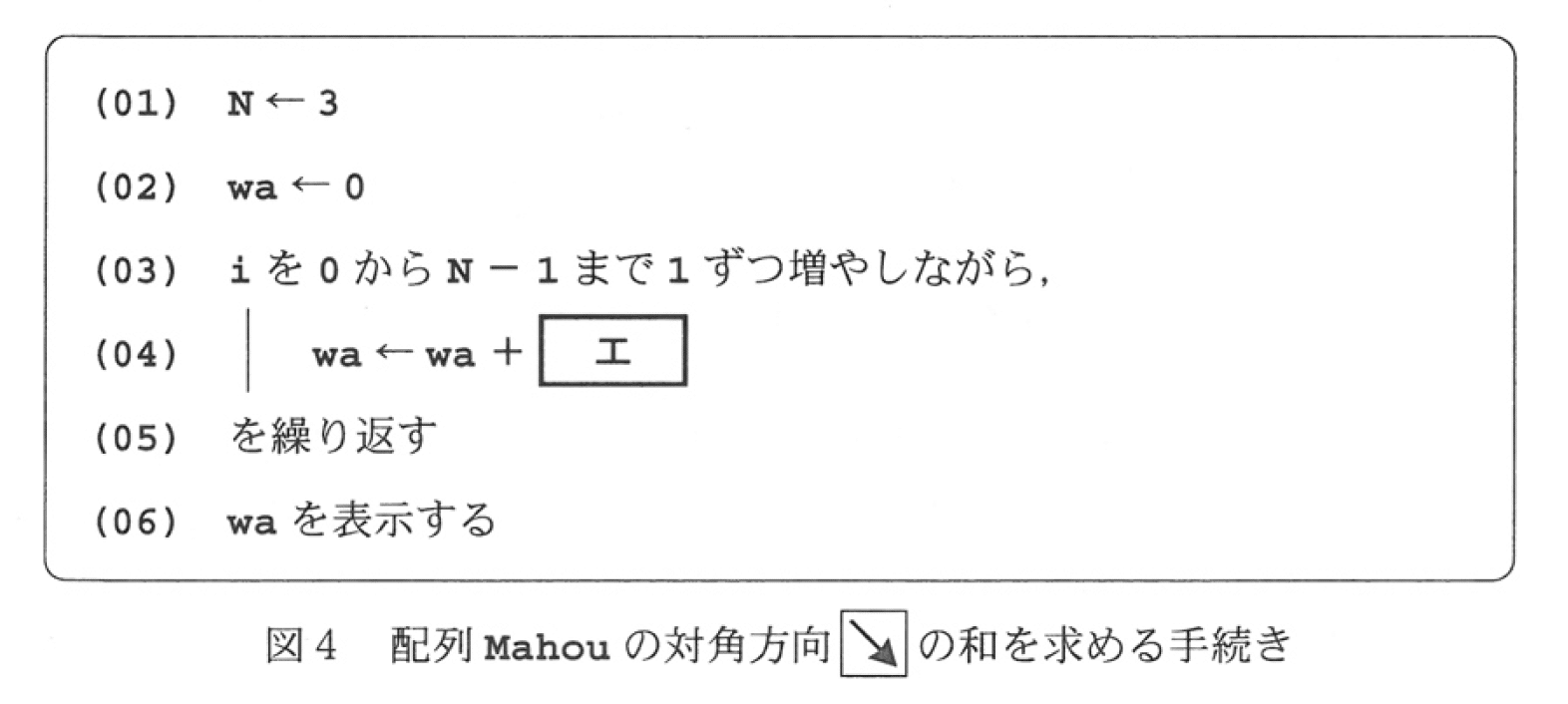
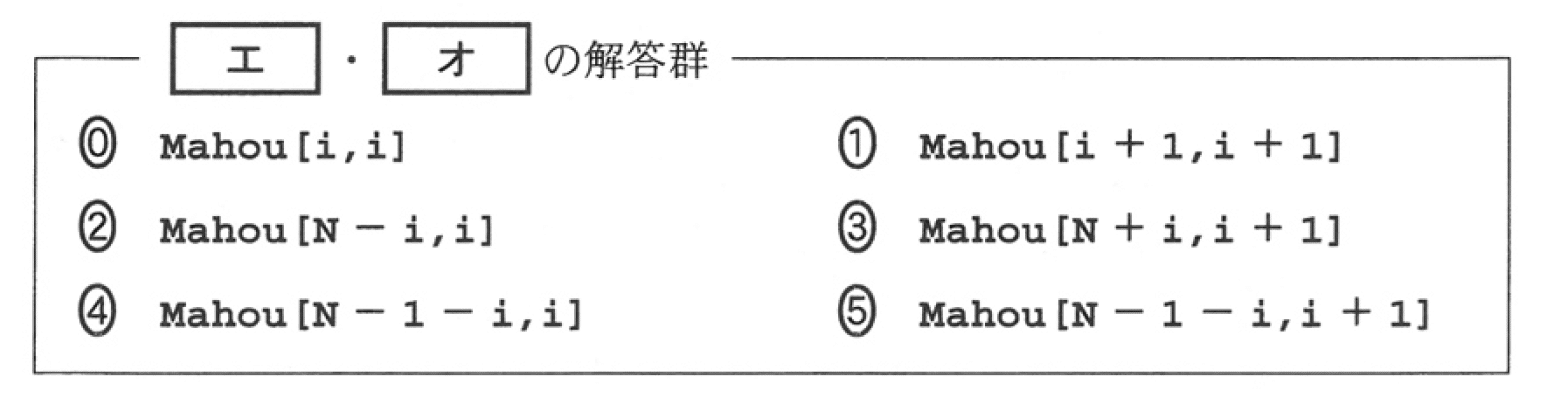
次は空欄の[ イ ]と[ ウ ]です．07行目でkizyunsuuを算出しています．さらにkizyunsuuを08行目で表示していますが，それ以降，この値を何らかの形で用いないと何のためにこれを算出したのかわかりません．ですので[ イ ]か[ ウ ]のいずれかはkizyunsuuであると考えられます．また10行目でmを変化させながら値を表示しているので，[ イ ]か[ ウ ]のいずれかは[m]が含まれるもの．つまり(7)か(8)になると考えられます．そうでないと同じ値が意味もなく繰り返し出力されることになってしまいます．また (7)のTomeiは文字列ですのでこれは明らかに割り算の被演算子としては不適です．つまり[ イ ]と[ ウ ]の正答は(8)と(b)の組み合わせであると予想できます．

ー　共通テスト「情報」最適化の原則　ー
繰返し文で配列の要素番号がインデックスなら0から(配列の要素数-1)まで1ずつ増やしながら繰り返すのが本命

ー　共通テスト「情報」最適化の原則　ー
初期化されていない変数が使われることはない

ー　共通テスト「情報」最適化の原則　ー
変数が代入されるだけで終わることはない

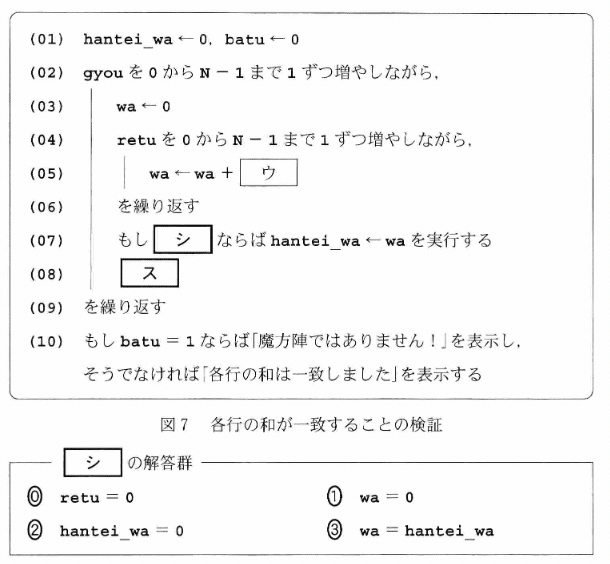
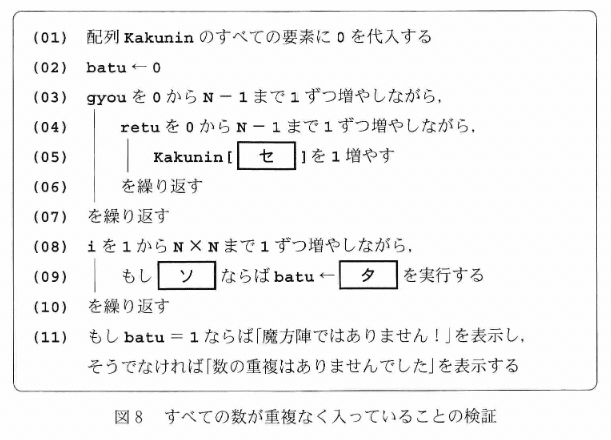
設問3

　同様に，[ セ ]〜[ チ ]をみてみます．プログラムと解答群は次の通りです．またいきなりプログラムと解答群だけですか？と驚かれていると思いますが，とりあえず見ていきましょう．

 

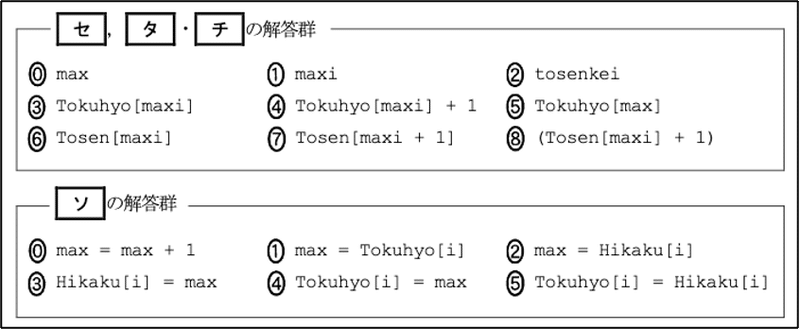
まず，[ セ ]です．これは(2)が正答とすぐわかります．なぜなら他の選択肢はmaxまたはmaxiのどちらかが含まれていますが，いずれの変数も1回目に行08が実行される時点では初期化されていないからです．

ー　共通テスト「情報」最適化の原則　ー
初期化されていない変数が使われることはない

次に[ ソ ]です．まずは，(0)〜(2)つまり代入先の変数がmaxであることはすぐわかります．なぜなら，09行max=0で代入されていますが，これ以降他の箇所で代入されていないからです．もしmaxが0という定数として扱われるのであれば，09行で代入せず，プログラム冒頭で初期値を代入するでしょう．さらに正答は(0)〜(2)の中で選ぶのであれば(2)だろうという推測もすぐできます．11行でmax < Hikaku[i] とあります．つまりmax と Hikaku[i] は値を比較できる同種の間柄であるということです．また，条件式で2項（ここではmax とHikaku[i]）比較し，何らかの条件を満たす場合は2項の一方（ここではHikaku[i]）をもう一方(ここではmax)に代入するような処理は頻繁に出現します．

ー　共通テスト「情報」最適化の原則　ー
冒頭で宣言されない定数ではなく変数なら，必ず値は更新される．

 

ー　共通テスト「情報」最適化の原則　ー
比較される変数間は代入されやすい．特に変数名にminやmaxが含まれるときはリーチ目．

 

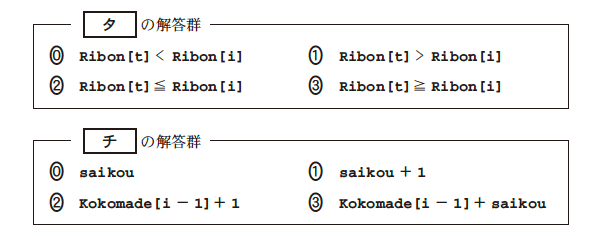
　次に，[ タ ][ チ ]です．図7の手順3にそのものが書かれています．ですので，[ タ ] は(3)，[ チ ]は(8)であることがわかります．

 

問題文で「プログラムの説明」と「題材となっているトピックのロジックの説明」と，どちらを表記するかは，今後の問題作成において検討すべき事項だと思います．どちらもあり得て，それにより測る能力や難易度が変わってきます．ただ，この問題の場合はプログラムの説明がそのまま図7に細かく記述されているために，対応する部分を見つけるだけで正答が得られてしまいます．

ー　共通テスト「情報」最適化の原則　ー
プログラムの説明に答えがまんま書かれていることがある．

実際にPICTOを使って実行させてみましょう．と言ってもPrinciples of Informatics of the Common Test Optimizationと少しフルスペルが違います．　筆者が開発しているピクトグラミングシリーズの一つでPICTO(Pseudocode for Informatics of Common Test Optimizer)という共通テスト用プログラム表記に準じたPython風の記法のビジュアルブロックをつなぎ合わせてプログラミングできるアプリケーションです．

https://pictogramming.org/からアクセスすることができます．

ちなみにPICTOで図9のプログラムを表示させる場合，こちらをクリックしてください．次のような画面が現れます．

 

設問2

　順番は逆転しましたが，[ エ]〜[ ス]を見てみましょう．ここ本来は図7のプログラムの説明の観点で書かれた手順に基づいて回答する想定となっていますが，問2冒頭の議席配分の方法について書かれた日本語文を中心に考えてみた方が良さそうです．

 

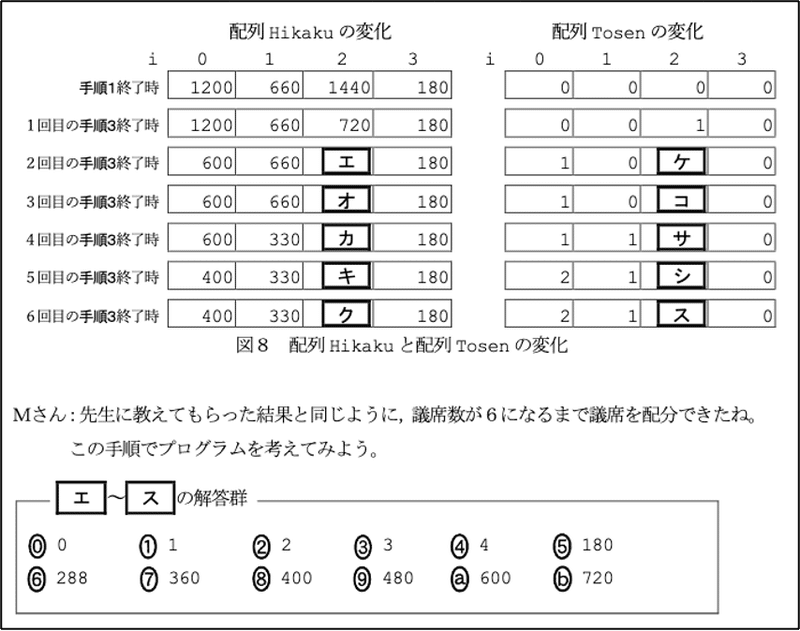
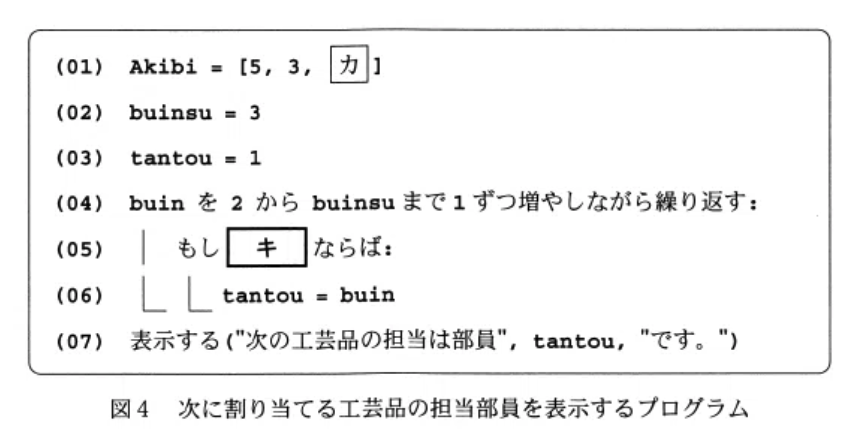
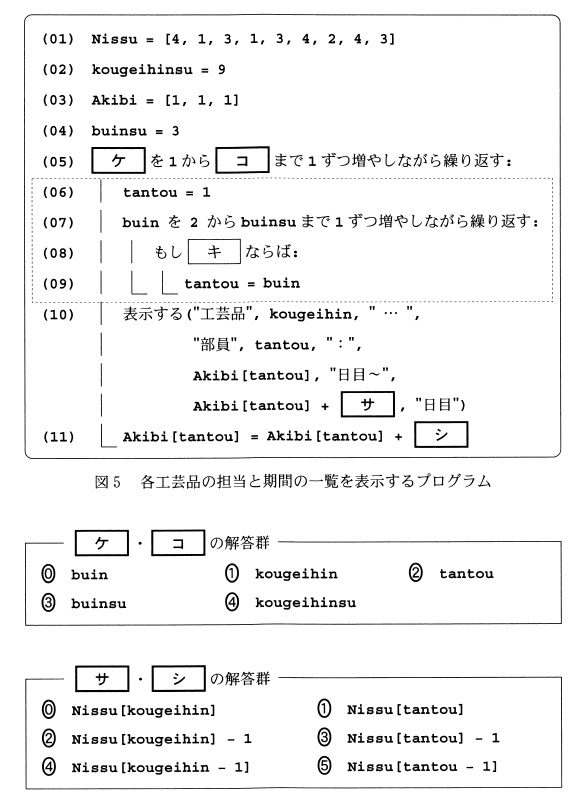
1回分の手順3終了が当選者を上位から順番に決めていくことに気づけば，C党は表2で❶，❸，❻，つまり1番目と3番目と6番目に当選しているので当選人数のTosen[2]は1回目と3回目と6回目で増えるはずです．よって[　ケ　]〜[　ス　]はそれぞれ(1)(2)(2)(2)(3)となります．手順2でTosen[2]の値が更新された後，手順3でHikaku[2] に「切り捨て(Tokuhyo[2]/ Tosen[2]+1)」 が格納されると述べているので，計算すれば[　エ　]〜[　ク　]はそれぞれ(b)(9)(9)(9)(7)となります．表2を見れば事前に[　エ　]〜[　ク　]は(7)(9)(b)しか入らないだろうことは予想がつきます．
また，実際の試験では2，3個埋めて他はグレイアウトされる形式ではないかと思います．今回のように10個全て空欄を埋める形式にはならないと思われます．

設問3（続き）

最後に[ツ]，[ テ ]です．

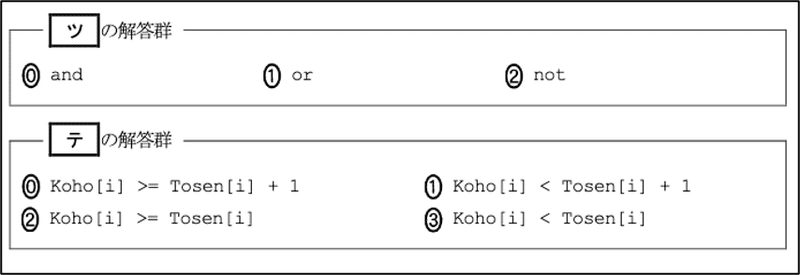
[　ツ　]は二項演算子が入るはずなので，(0) andか(1) orです．orだとするとこれまでの条件だった max < Hikaku[i] の条件を満たさなくても行11 の条件式全体が真になる場合が発生します．条件を追加するわけですので，(0)が正答と予想できます．
[ テ ]は，条件式におけるKoho[i]とTosei[i]の大小比較です．選択肢が全てKoho[i]とTosei[i]に関する値の大小比較なので，当てはめが有効そうです．Koho[i]とTosei[i]は，候補者数と当選者数なので，いずれも0以上の整数です．候補者が無限（∞）にいる場合は[ テ ]は常に真となるするはずです．(1)は ∞ < Tosen[i] + 1, (3)は ∞ < Tosen[i] となりますので，不適です．一方候補者が一人もいない場合(0人)は常に偽となるはずです．(2)はTosen[i]が0のとき，真になってしまうので，これも不適であることがわかります．よって正答は(0)です．
以上になります．

ー　共通テスト「情報」最適化の原則　ー
解答群の選択肢が似ているなら当てはめてみる．

 

 

試作問題2022（令和4年11月9日公開）をPICTOで解いてみる．

2025年度入試(2025年1月実施予定)から教科「情報」が共通テストに追加されます．すでに大学入試センターから試作問題2022（令和4年度11月9日公開）が出ています．では次にこの試作問題2022を見ていきましょう．

この第3問（22ページから27ページ）がプログラミング，アルゴリズムの問題です．この問題を実際に解いてみたいと思います．

以下，画像引用は上記PDF からの引用になります．

　まずいきなりですが，図1から見てみましょう．え！いきなりプログラムと解答群から見るんですか？と驚かれるかもしれません．この図1のプログラムに関して「共通テスト「情報」最適化の原則　変数の単位に着目してみる」　から見ていきます．

 

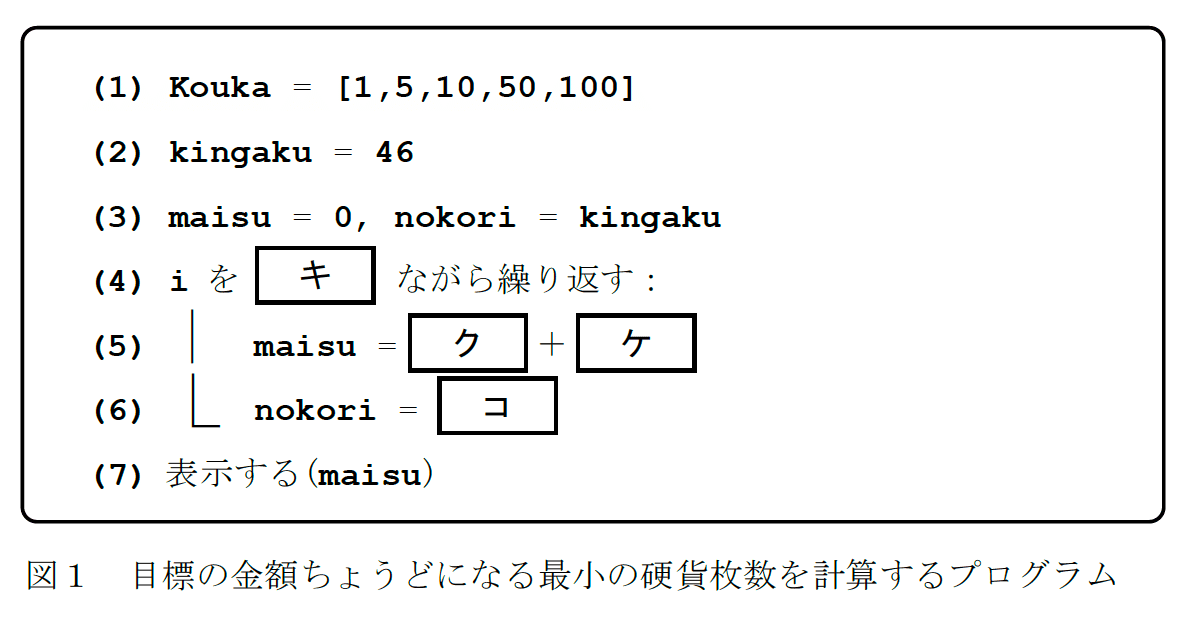
まず[ キ ] です．変数iがありますが，これは変数名から配列のインデックスであるとわかります．この問題では，配列はKoukaだけで，そのインデックスに相当するとわかります．共通テストの仕様では，配列のインデックスは0オリジン（0から始める）です．よって0と4が含まれる(1)か(2)が正答であることはわかります．一見(2)が本命ですが，まだこの時点では確定できません．
次に[ク]です．ここで，配列の要素，変数の単位系を考えてみましょう．配列や変数の名前から推測してみます．

ー　共通テスト「情報」最適化の原則　ー
変数や配列の要素の値の単位が何になるか考えよ．

Kouka = [1,5,10,50,100] とあり，硬貨のそれぞれの種類の額からなる配列というは見てすぐイメージできます．図1のキャプションにも「目的の金額ちょうどになる最小の硬貨枚数を計算するプログラムとあります．」．なのでKoukaの単位は円です．同様にkingakuも円，maisuは枚数なので枚でしょう．nokoriはこの名称からだけではわかりませんが，行(3)のnokori = kingaku から残りkingakuとnokoriの単位は同じ．つまりnokoriは残り金額（円）と判断できます．
行(5)でmaisu = [ク] + [ケ]　です．右辺は+なので，[ク]も[ケ]も単位は左辺のmaisuと同じ，枚と考えられます．[ク]の選択肢を見ると，(0) 1 [不明], (1) maisu [枚] ,(2) i [単位なし], (3) nokori [円] ですから，(0)か(1)です．

次に[ケ]と[コ]について考えてみましょう．[ケ]の単位は枚でした．[コ]の単位は，そう，円です．

そもそも[ケ][コ]の選択肢の単位が何になるのかそれぞれ考えましょう．A÷Bの単位は　(Aの単位)/(Bの単位) A%Bの単位はAになります．
(0) 円/　1枚当たりの円 = 枚
(1) 円
(2) 枚/ 1枚当たりの円　= ?
(3) 枚

ー　共通テスト「情報」最適化の原則　ー
変数や配列の要素の値の単位が何になるか考えよ．

ー　共通テスト「情報」最適化の原則　ー
ある変数の値がある変数に代入されるならば単位はたぶん同じ．

まず[コ]の正答が(1)と確定しました．[ケ]は，ここまでの議論で(0)か(3)です．ただ，行(5)と行(6)の繰り返しの中で行(6)でnokoriに値が代入されています．そのnokoriは行(5)でmaisuに値を代入するとき必ずなんらかの形で関与しています．そうしないとnokoriに値を代入した意味がないからです．なので，[ク][ケ]のいずれかにはnokoriが含まれています．[ク]にはnokoriが含まれていません．[ケ]にnokoriが含まれるので，(0)となります．

ー　共通テスト「情報」最適化の原則　ー
変数になんらかの値が代入されただけでは終わらない．

最後に，[ク]を考えます．ここで，[ケ]と[コ]はいずれもmaisuが含まれないことがわかりました．よって，[ク]にmaisuが含まれていないと繰り返し処理の中でmaisuを更新する意味がありません．よって[ク]は(1)maisu　となります．

次に図2を見ていきましょう．
またいきなりプログラムと解答群だけですか？と驚かれていると思いますが，とりあえず見ていきましょう．今度は，図1と別のPICTO も使って解いていきましょう．

 

 

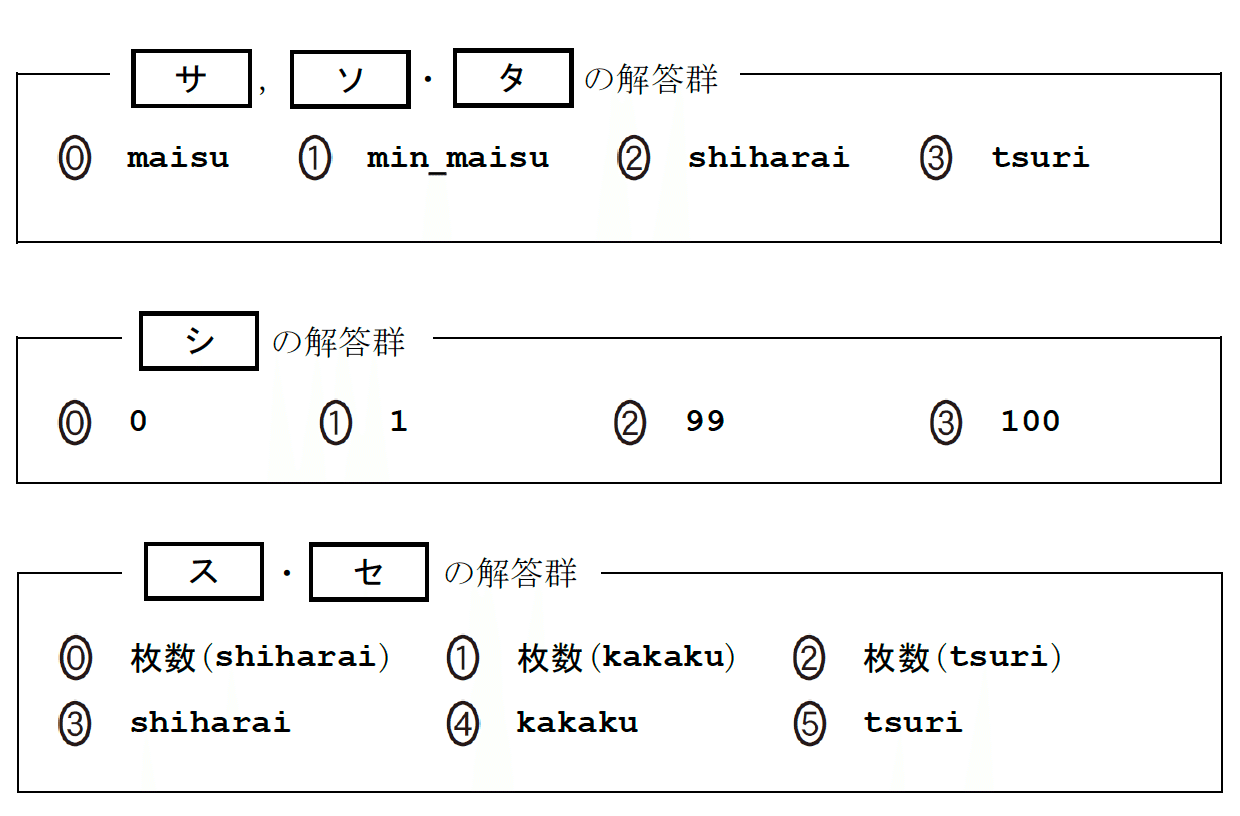
まず[サ]です．これは，一見で(3)tsuri が正解とわかります．行(3)は繰り返し文ですが，[サ]に対して順番に値を格納していく代入文とも言えます．するとkakaku, min_maisu, maisu は連続して代入されていることになります．値が連続して代入される処理にというのは不自然です．次の原則に則ります．

ー　共通テスト「情報」最適化の原則　ー
変数が連続代入されることはない

ー　共通テスト「情報」最適化の原則　ー
初期化されていない変数が使われることはない

[シ]は(0)か(1)です．繰り返し文が定義されているということは，2回以上繰り返されることが想定されるからです．

次に[ソ]にいきましょう．min_maisuと比較している変数であるはずです．min_maisuの単位は変数の名称から枚と考えられます．(1)だと，min_maisu < min_maisu となって明らかにおかしいので，よって(0)のmaisuとわかります．[タ]も同様に　[タ] = maisu なので，[タ]の単位は枚です．よって(1)のmin_maisu となります．

ー　共通テスト「情報」最適化の原則　ー
変数と変数が比較されるならば単位はたぶん同じ．

最後に[ス][セ]です．maisu = [ス] + [セ]　なので，[ス]も[セ]も単位は枚です．(3)shiharai,(4)kakaku,(5)tsuri はいずれも円です．関数 枚数(XXX)はXXX（単位は円）を与えると何らかしらの枚数を返すものだと思われます．よって，選択肢(0)-(2)のいずれかが正答とわかります．[ス][セ]は順不同ですが，いずれかは(0)枚数(shiharai)とわかります．なぜなら選択肢(0)がないと，行(4)で変数shiharaiが代入されたのに使われないからです．もう一方は，(0)ではありません．maisu = 枚数(shiharai)+枚数(shiharai)なら，普通maisu = 2 * 枚数(shiharai)と書くはずです．よって (1)か(2)です．

最後に

以上が，PICTOによるサンプル問題と試作問題2022の解説でした．

 

『共通テスト「情報」最適化の原則』という名称（略称ピクト）で連載し始めてしまいましたが，ニーズがあれば連載いきたいと思います．なぜ略称がピクトかと言いますと，英語表記がPICTO ：Principles of Informatics of the Common Test Optimization）だからなのと，私が開発・運営しているピクトグラミングに語呂をかけています．

今回は，2024年度共通テスト「情報関係基礎」のプログラム問題を題材に，PICTO式でプログラム問題を見てみたいと思います．情報関係基礎の過去問は，情報処理学会情報入試委員会のサイト内の「情報関係基礎　アーカイブ」からダウンロードできます．こちらを参照ください．共通テスト「情報」で採用されるのは「共通テスト用プログラム表記」で，「情報関係基礎」で使用されているDNCLとは異なるものであることは留意ください．

2024年度共通テスト「情報関係基礎」のプログラミング問題をPICTOで解いてみる．

早速，問題を見ていきましょう．
第3問（問題冊子38ページから43ページ）がプログラミング，アルゴリズムの問題です．この問題を実際に解いてみたいと思います．

ある程度作問経験が豊富であると，このトピックならこういう問題になるだろうことは予想できます．問題のトピックは魔方陣でした．共通テスト「情報関係基礎」の問題フォーマットの制約や，想定される回答標準時間を考慮すると，魔方陣のトピックで問題を作ることはあまり筋が良くないように思えます．次のような理由が主に挙げられます．

1．同じようなことを繰り返し問う設問群にならないか．
2．魔方陣作成方法を問う場合で，穴あけ形式の問題により対応するプログラムが完全なものでないと，その手順の説明を日本語で詳細にしなければならない．その結果，仕様やアルゴリズムについて日本語で記述された文章の読解力のみで解答できてしまうことがある．ただし，それを意図して作問されることはありうる．
3．魔方陣の作成方法は，それなりに知られており，それを経験したことがある人は，方法を理解する時間が省けて有利になる．
4. 想定されるプログラムが比較的単純なため，穴埋め問題形式の選択肢が作りにくく，その結果テクニックで正答が導けてしまう．

それでもこのトピックを採用した理由の一つに，0オリジンの配列を扱う問題を提示したいという思惑があったと考えられます．情報関係基礎の擬似コード仕様の場合，0オリジンか1オリジンかは明記されていません．ただ過去問題をみると1オリジンの方が圧倒的に多いです．例えば，n行目とかn文字目とかいうと普通1オリジンが普通であり，1オリジンだとn文字目の文字をMoji[n]と定義できます．一方で0オリジンにするとn文字目の文字がMoji[n-1]となり，このnとn-1の対応で混乱したり，（ケアレスミスで）誤答を選んでしまうということが発生するからです．ただ例外はいくつかあり，今回のようにトーラス状のグリッドを扱うようなテーマの場合，剰余を扱うので0オリジンで扱われる方が理解しやすいです．つまり，0オリジンにして0行目，0列目を定義した方がよりわかりやすく自然な処理となります．共通テスト「情報」で採用される共通テスト用プログラム表記では0オリジンとなっています．

問1

　まずいきなりですが，図2から見てみましょう．え！いきなりプログラムと解答群から見るんですか？と驚かれるかもしれませんが，とりあえず見てみましょう．

 

PICTO（Pseudocode for Informatics of the Common Test Optimizer）を使用して，プログラムを実行してみる場合，次のリンクをクリックしてください．
図2のプログラムをPICTOを使って開く

 

ループ変数retu を使って変数waに[ウ]を繰り返し足しています．行04から06はもしretuを含まないのなら，
wa ← N × [ ウ ] で良いはずです．なのに繰り返しを使用しているということは，[ウ]はretuが含まれている(1)か(2)です．さらに1回目の繰り返し（retuが0のとき）を考えてみると，(2)では，Mahou[-1, gyou] と配列要素の数値が負(-1)になってしまいます．よって[ウ]の正解は(1)です．

ー　共通テスト「情報」最適化の原則　ー
繰り返し文は1回目の繰り返しを考えて当てはめてみる．

ー　共通テスト「情報」最適化の原則　ー
本番時ではなく学習時は，誤答を当てはめた時に，プログラムが不自然になることを意識し，どう不自然になのか考えてみる．

　同様に，図4と[ エ ]の選択肢をみてみます．プログラムと解答群は次の通りです．またいきなりプログラムと解答群だけですか？と驚かれていると思いますが，とりあえず見ていきましょう．

図4のプログラムをPICTOを使って開く

 

ー　共通テスト「情報」最適化の原則　ー
繰り返し文は1回目の繰り返しを考えて当てはめてみる．

ー　共通テスト「情報」最適化の原則　ー
繰り返し文は最後の繰り返しを考えて当てはめてみる．

ー　共通テスト「情報」最適化の原則　ー
図表のキャプションにヒントあり！

上記2つを併用すると，解答の候補としては(0)(4)しかあり得ません．[エ][オ]は(0),(4)か(4),(0)かのいずれかですね．図4のキャプションと図3を見ると[エ][オ]は(0),(4)が正答のようです．図のキャプション文字列に問題を解く上でのショートカットが潜んでいることが多々あります．

問2

まずいきなりですが，図5,6及び図の解答群から見てみましょう．え！いきなり 図とプログラムと解答群から見るんですか？と驚かれるかもしれませんが，とりあえず見てみましょう．
PICTOを使用して，プログラムを実行してみる場合，次のリンクをクリックしてください．
図6のプログラムをPICTOを使って開く

 

図5の(a)から数値1が入っているのはx=1,y=2です．Nは3です．N=3のときも成立するはずですから当てはめましょう．解答群[カ][キ]の選択肢にN=3を当てはめると
(0) 0 (1) 3 (2) 2 (3) 4 (4) 1 (5)0
ですので[カ]は(4)，[キ]は(2)ですね．普通は当てはめ対策としてNが3を代入したときに値が1や2になるものを複数作るもののですが，この問題ではそれもしていません．
図5の(b)から数値2が入っているのはx=2,y=0です．行04からループの初めのzが2で，10行目でMahou[x,y]←zとなっているのでループの1回目は2を入れるための処理です．[ケ]と[コ]が実行されるときのx,yはそれぞれ1,2ですから
[ケ]と[コ]の選択肢に当てはめます．
(0) 1-3=-2 (1) 1+3 = 4
(2) 1 % 3 = 1 (3) (1+1)%3 = 2
(4) 2-3 = -1 (5) 2 % 3 = 2
(6) (2+1)%3=0 (7) 1+2-1=2

[コ] は0にならないといけませんから(6) (y+1)%N です．さらに [ケ]は(3),(5),(7)の3通りが考えられますが，(6) (y+1)%Nとの対比を考えると(3) (x+1)%N　が正しそうです．
ここまでで，zが1増えるごとに（トーラス状で）右下へ次の番号が書かれるのがわかります．図5の(d)では次の文字が一つ上でに書かれているので，これが，8行目の処理に相当すると考えられます．一つ上なので，[サ]は(5)y←y-1となります．

 

魔方陣を作成する手順の部分は，実際には問題文で曖昧性が生じないように厳密に書かれるので，対応するプログラムが穴あけ方式だと，日本語読解問題になりがちで，本問も日本語で書かれている説明文を読めばいいですが，あえてそれなしに解くことをしてみました．例えば図6のプログラムが穴あけされていない完全なプログラムの場合，魔方陣を作成する手順の説明なしにプログラムの挙動を問うことができます．こういう形式の問題はページ制約の関係から情報関係基礎ではなかなか難しそうですが，共通テスト「情報」では出てくると思います．

ー　共通テスト「情報」最適化の原則　ー
プログラムの説明に答えがまんま書かれていることがある．

 

問3

まずいきなりですが，図7から見てみましょう．え！いきなりプログラムと解答群から見るんですか？と驚かれるかもしれませんが，とりあえず見てみましょう．

PICTO(Pseudocode for Informatic of the Common Test Optimizer)で実行する場合はこちらをクリックしてください．

まず[シ]です．（0）が正答でないのはすぐわかります．繰り返しで使うループ変数は，特に擬似言語の場合にはループ外でどういう値になっているかは不定です．作成側に関する話ですが本当は(0)のような選択肢は作るべきではありません.
(1)も変です．(06)までの処理でN=3のケースではwaは15になっているはずなので，そのwaを0と比較するのも変だからです．(3)も変です．もしwaとhantei_waが等しいなら，実行されるhantei_wa ← wa は意味がない（同じ値を代入するので）ことになってしまいます．よって(2)が正答です．

次に[ス]です．プログラム中でbatuが更新されるとすると[ス]だけですが，0以外の値が代入されるのは(2)以外です．(2)だとbatuが全く更新されないことになってしまうのでわざわざbatuを定義しなくても0でいいということになってしまいます．さらに実は(1)と(3)は同じことを言っています．つまり(1)がもし正解なら(3)も正解になります．よって(0)が正解です．

ー　共通テスト「情報」最適化の原則　ー
実質的に同ーの処理が別の選択肢にもあるなら，それは正答ではない．

 

図8のプログラムをPICTOで実行する場合は，こちらをクリックしてください．

まず[セ]です．Mahou[ , ]が参照される場所は，考えられるのはこの部分だけです．もしここでMahou[,]を参照しなかったら，数の重複があることを調べることすらできません．よってMahouを含むはずです．あとは，retu, gyouの繰り返しの中の処理なのでretu, gyouはともに1回は参照されるはずです．参照されなければ，もっと自然な別の書き方があるはずです．よって (4) Mahou[retu, gyou]が正解です．

[タ]は解答群がありませんので，一桁の数字を選びます．(02)行でbatuに0が代入されていて，(11)行でbatuが1か判定しています．9行めしかbatuの値が変更しないので，1が正答とわかります．
さて最後に[ソ]です．結局Kakunin[i]には魔方陣全体でiの値が現れる回数が格納されていることがわかります．1以上N^2の全てのiに対して，Kakunin[i]=1 なので，(3)が正解とわかります．

 

 

 

 

 

 

『共通テスト「情報」最適化の原則』という名称（略称ピクト）で連載していきます．なぜ略称がピクトかと言いますと，英語表記がPICTO ：Principles of Informatics of the Common Test Optimization）だからなのと，私が開発・運営しているピクトグラミングに語呂をかけています．

今回は，2023年度共通テスト「情報関係基礎」のプログラム問題を題材に，PICTO式でプログラム問題を見てみたいと思います．情報関係基礎の過去問は，情報処理学会情報入試委員会のサイト内の「情報関係基礎　アーカイブ」からダウンロードできます．こちらを参照ください．
共通テスト「情報」で採用されるのは「共通テスト用プログラム表記」で，「情報関係基礎」で使用されているDNCLとは異なるものであることは留意ください．

 

2023年度共通テスト「情報関係基礎」のプログラミング問題をPICTOで解いてみる．

早速，問題を見ていきましょう．
第3問（問題冊子36ページから41ページ）がプログラミング，アルゴリズムの問題です．この問題を実際に解いてみたいと思います．

問1

　まずいきなりですが，図2から見てみましょう．え！いきなりプログラムと解答群から見るんですか？と驚かれるかもしれませんが，とりあえず見てみましょう．

Picthon (ピクトグラミング　Python: テキスト型)を使用してプログラムを実行してみる場合は，次のリンクをクリックしてください．
図2のプログラムをPicthonを使って開く

まず空欄[カ]から．図2のキャプションに5mずつ降りるとあるのでおそらく(3) takasa-5 が正解だと思われます．
次に空欄[オ]です．(0)は常に偽，(3)は常に真になりますので誤答でしょう．(1)はtakasa-5以上takasa以下にRibon[i]がない．(2)はあるです．この時得点(score)が1足されます．ということは100%確定はできませんが，5m降りる間にRibonがあれば得点が1増えるという(2)が正解と思われます．また図のキャプションから，takasaの単位はmだろうとわかりますが，[オ]の選択肢からRibon[i] とtakasaを比較しているので，Ribonの配列も単位がmの値が格納されていることがわかります．

ー　共通テスト「情報」最適化の原則　ー
図表のキャプションにヒントあり！

ー　共通テスト「情報」最適化の原則　ー
解答群の選択肢が似ているなら当てはめてみる．

 

問2

　いきなりですが，図3から見てみましょう．
Picthon (ピクトグラミング　Python: テキスト型)を使用してプログラムを実行してみる場合は，次のリンクをクリックしてください．
図3のプログラムをPicthonを使って開く

問1からRibon[i]の配列要素は1オリジンで11要素あるようです．極端な例を考えてみたいと思います．問1で得点が最高点(11点)になるケースのRibon[i]を考えてみてください．いかがでしょう．例えば、
Ribon = [52, 47, 42, 37, 32, 27, 22, 17, 12, 7, 2] は満たしますね．
これまで11点だったものが「新しい動かし方」でよりスコアが低くなってしまうとは考えにくいです．このようなスコアの獲得を題材とした問題の場合，設問を経ることで，より方策やアルゴリズムが最適化していくというのが良くあるパターンです．すると[　ク　]は各繰り返しで常に成立しますので，この前提下で[　ケ　 ]のtakasaはどのように更新されていくでしょうか？
(0) 55,52,47,42,…
(1) 55,107,154,196,…
(2) 55, 3,-44,-86,…..
(3) 55, -3, 50 , -8
設問1はtakasaが55,50,45,40,35…. と5mおきに下がっていました．これと動かし方が大きく変わるとは考えにくく，おそらく正答は(0)である可能性が高いと推測することができます．

 

ただし，いずれもこれだけでは100%の確証をもって正答は導けません．以前解説した，試作問題2022や2024年度情報関係基礎の問3とは異なり，プログラムを見ただけでは解を絞ることができません．通常はこのような，先に提示したショートカットだけでは解けない問題が共通テストのプログラム問題では出題される（少なくても2025年から3,4年の間は）と考えるのが妥当です．では，（プログラムではない）図と表を見てみましょう．

 

この図1を見ると先ほどの[　ケ　]は，なおさら(0)が妥当に見えます．takasaが取りうる値がマイナスになったり55よりはるかに大きくなることはなさそうです．

問3

　いきなりですが，図4から見てみましょう．また設問1，2と同様に極端な例を考えてみたいと思います．

Picthon (ピクトグラミング　Python: テキスト型)を使用してプログラムを実行してみる場合は，次のリンクをクリックしてください．
図4のプログラムをPicthonを使って開く

 

新しくsaikouという変数と，Kokomadeという配列が出現しました．先ほどの設問1，2で獲得得点の最高は11で，どうも図1からリボンを触れるか取るかした個数のような気がします．まずは，行5の条件式が常に不成立と仮定して，[　チ　]の回答群を当てはめたときにKokomadeの配列の値がどうなるか考えてみましょう．
(0) 1,0,0,0,0,0,0,0,0,0,0
(1) 1,1,1,1,1,1,1,1,1,1,1
(2)1,2,3,4,5,6,7,8,9,10,11
(3) 1,1,1,1,1,1,1,1,1,1,1

次に行5の条件式が常に成立と仮定して[　チ　]の回答群を当てはめたときにKokomadeの配列の値がどうなるか考えてみましょう．
(0) 1,1,1,1,1,1,1,1,1,1,1
(1)1,2,3,4,5,6,7,8,9,10,11
(2)1,2,3,4,5,6,7,8,9,10,11
(3) 1,2,4,8,16,32,64,128,256,512,1024

(0)と(3)は論外，(1)と(2)なら変化があり常偽，Kokomade[11]が1と11になる(1)が正答のように思えます．このように条件文をとりあえず常に真，常に偽として処理してみるというのは一つ正答を推察する方法です．もちろんこれだけでは100%の確証をもって正答は導けません．

ー　共通テスト「情報」最適化の原則　ー
条件式を常に真，常に偽と仮定することで単純化して解いてみる．

普通問題というと先頭から順に読解していきたくなります．これは問題の形式に依存はするのですが，共通テスト「情報」のプログラム問題のケースでは，「プログラム（選択肢含む）」→　「図表」 → 「自然言語による説明文」　の順に参照していくのが良さそうに見えます．実際の入試では，さすがにリード部分（問題の最初の一文や一文節）ぐらいは最初に読んで，問題が扱っているテーマを把握することは必須です．
日頃練習問題として解く場合は，「プログラム（選択肢含む）」→　「図表」 → 「自然言語による説明文」の順に参照し，「プログラム（選択肢含む）」だけ，あるいは「プログラム（選択肢含む）」と「図表」だけで正答が定らない場合，どの情報が不足していて，自然言語による説明文にどのような説明が記述されているだろうとイメージしてみるというのが良さそうです．

ー　共通テスト「情報」最適化の原則　ー
日頃から，「プログラム（選択肢含む）」→　「図表」 → 「自然言語による説明文」の順に参照し，あとどの情報があれば正答が確定できるかを想定しながら解く．

闇雲に問題を解き，なんかそれっぽく解説している解説文を読む．そんな問題の解き方，受験勉強の仕方から脱却しませんか？それは，教科「情報」が醸成しようとしている能力の一つな気もします．質の良い共通テストの教科「情報」の問題は，さまざまな記号体系（自然言語，図表，プログラム（選択肢含む））が融合した一種の芸術作品のようになると思います．ただ現状あまりそのような良質な問題がなく，質の悪い問題も少なくないので，教科「情報」の受験勉強は，それを見定める一種の活動とみなしても良いのかもしれません．それがもしかしたら，共通テストの問題を題材にいっそのこと「楽しんでしまおう」というヒントにもなると思います．

 

第8回目となる今回は，共通テスト教科追・再試験「情報I」のプログラム問題を解いてみたいと思います．

問題（令和7年1月26日実施）PICTO式で解いてみる．

では問題を見ていきましょう．
この第3問（22ページから27ページ）がプログラミング，アルゴリズムの問題です．この問題を実際に解いてみたいと思います．

設問1

　まずいきなりですが，図2から見てみましょう．え！いきなりプログラムと解答群から見るんですか？と驚かれるかもしれませんが，とりあえず見てみましょう．

さて，空欄[  ア  ][ イ ]を考えてみましょう．解答群を見ると，まず添え字の番号が1,2,nで分かれています．キャプションに一人分の結果を各配列に格納するプログラムとあります．ということは，Iremono,Shurui,Keiryouの対応する添字の番号に順に入れるので，nが本命だと思われます．(05)行で種類と書いてありますので，空欄アは(5)，同様に(07)行で軽量と書いてありますので，空欄イは(8)でしょう．

ー　共通テスト「情報」最適化の原則　ー
変数が連続代入されることはない

 

設問2

　まずいきなりですが，図4から見てみましょう．え！いきなりプログラムと解答群から見るんですか？と驚かれるかもしれませんが，とりあえず見てみましょう．

 

まず[　ウ　]を考えてみましょう．(01) 行で代入されたninzu（単位は人）は使われるとしたら，[　ウ　][　カ　][　キ　]　のいずれかですが，[　カ　][　キ　]はいずれも単位がgです．足し算の場合，全ての項は単位が同じになるはずです．よって[　ウ　]は(4) ninzu です．原則はもう頻出の以下のものですね．

ー　共通テスト「情報」最適化の原則　ー
変数や配列の要素の値の単位が何になるか考えよ．

ー　共通テスト「情報」最適化の原則　ー
ある変数の値がある変数に代入や比較されるならば単位はたぶん同じ．

ー　共通テスト「情報」最適化の原則　ー
定義されている変数，配列が使われないことはない

 

[　カ　][　キ　]は繰り返しの中で使われていますが，いずれも変数kanen,
funen　の代入文の右辺にそれぞれ kanen, funen が含まれていないと，連続代入になってしまいます．よって [　カ　]は(5) kanen, [　キ　]は(6)funenです．

ー　共通テスト「情報」最適化の原則　ー
変数が連続代入されることはない

次に[　エ　][　オ　]に行きましょう．図2からIremono[i] もShurui[i] もなんらかの名称で表現されるモノを割り当てた数値（単位なし）です．比較されるということは単位は多分同じです．よって，(2)(5)は除かれます．図2からShurui[i] == 1 だと可燃ごみで，Shurui[i] == 2 だと不燃ごみと書かれているので，変数名kanen,funenとの対比を考えると[　オ　]は(3)Shurui[i] == 1 が濃厚です．また，図2から，Iremono[i] == 1 だとバケツで，Iremono[i] == 2 だとゴミ袋と書いてあるので，おそらく350はバケツの重さで，[　エ　]の正答は，(0) Shurui[i] == 1 が濃厚です．

ー　共通テスト「情報」最適化の原則　ー
変数と変数が比較されるならば単位はたぶん同じ．

 

設問3

　まずいきなりですが，図5から見てみましょう．え！いきなりプログラムと解答群から見るんですか？と驚かれるかもしれませんが，とりあえず見てみましょう．

ではやってみましょう．
ちなみに[　ア　]はIremono[n]です．[　ク　]から行きましょう．

ー　共通テスト「情報」最適化の原則　ー
定義されている変数，配列が使われないことはない
ー　共通テスト「情報」最適化の原則　ー
変数や配列の要素の値の単位が何になるか考えよ．

 

からもうわかりますね．[　ク　]が(1)shuruisuです．[　ケ　]は

 

ー　共通テスト「情報」最適化の原則　ー
ある変数の値がある変数に代入や比較されるならば単位はたぶん同じ．

 

を考えると，(07)行の左辺は，ゴミの種別を番号で表したものなので単位はないです．単位がない（というかループ変数で何にでもなりうる）のは，(0) j です．

次に，図6を見てみましょう．え！いきなりプログラムと解答群から見るんですか？と驚かれるかもしれませんが，とりあえず見てみましょう．

 

 

共通テスト「情報」最適化の原則　を適用すれば，
[　コ　]は(4) Shurui[i]，[　サ　]は(c)Goukei[s]，[　シ　]は(8) Namae[j] ，[　ス　]は(b) Goukei[j]であることを導くのは難しくありません．どれを適用すれば良いのか考えてみてください．

最後に

以上が，2025年度共通テスト追・再試験「情報I」のプログラム問題の解説でした．一見テクニック集かと思われるかもしれませんが，いずれもデバッグやリファクタリングの際に行なっているプログラミングの自然な行為なのです．今回の試験では，本試験に引き続き1オリジンの配列が使われました．事前では，0オリジンの配列がデフォルトと思われていたので，少し混乱も見られたようです．しかしながら作問チームがあえて1回目の試験で，1オリジンの配列を適用してきたのは，メッセージとしては妥当かと思えます．

 

第7回目となる今回は，共通テスト教科本試験「情報I」のプログラム問題を解いてみたいと思います．

 

問題（令和7年1月19日公開）PICTO式で解いてみる．

 

では問題を見ていきましょう．
この第3問（22ページから27ページ）がプログラミング，アルゴリズムの問題です．この問題を実際に解いてみたいと思います．

設問2

　まずいきなりですが，図4から見てみましょう．え！いきなり設問1も飛ばして，プログラムと解答群から見るんですか？と驚かれるかもしれませんが，とりあえず見てみましょう．プログラムを実行されたい場合は 図4のプログラム をクリックしてください．

 

今回の試験では，1オリジン（要素番号が1から始まる）の配列が使われました．事前では0オリジンの配列がデフォルトと思われていたので，少し混乱も見られたようです．しかしながら，作問チームがあえて初回の試験で，1オリジンの配列を使用してきたのは，メッセージとしては妥当かと思えます．この問題の場合，1オリジンの部員番号，工芸品番号を扱う際に0オリジンとすると添字に-1がつくことになり，そのズレが原因で，受験者が凡ミスで別の解答を選択する懸念があるからです．以前の「情報関係基礎」の試験では1オリジンで扱うことが通常でした．作問者からすると当然の配慮かと思います．

さて，空欄[　キ　]を考えてみましょう．配列Akibiは他のところで一切参照されていません．使われるとするとこの部分になります．よって正答は(1)か(3)ですが，そのいずれなのかはこれだけではわかりません．ただし，このプログラムと図のキャプションから「担当部員は三人いる．それぞれの担当部員にはAkibiという値が設定されている．最もAkibiの値が小さいか最もAkibiの値が大きい担当部員が工芸品を割り当てられる．どちらなのかは，この位置より前のどこかに文章で指定されているはずだ．」この情報を把握してから問題中の自然言語で書かれた文章を読む，つまり解答するのに必要な目的を知ってからその情報が含まれる文を全体から探すのと，そうでなくとりあえず仕様把握を目的に全体をくまなく読むのでは効率が変わってきます．

ー　共通テスト「情報」最適化の原則　ー
繰返し文で配列の要素番号がインデックスで1オリジンなら1から(配列の要素数)まで1ずつ増やしながら繰り返すのが本命

ー　共通テスト「情報」最適化の原則　ー
定義されている変数，配列が使われないことはない

ー　共通テスト「情報」最適化の原則　ー
先にプログラムを読むことで，結果自然文章で書かれている仕様把握が早くなる．

 

 

 

まず[　コ　]を考えてみましょう．次の2つの原則から，[　コ　]は(4)か(3)かと思われます．

ー　共通テスト「情報」最適化の原則　ー
変数が連続代入されることはない

ー　共通テスト「情報」最適化の原則　ー
初期化されていない変数が使われることはない

また，次の原則を使って考えてみます．

ー　共通テスト「情報」最適化の原則　ー
変数や配列の要素の値の単位が何になるか考えよ．

buinsuは人，buin, tantou は人を識別するための番号，kougeihinsuuは個，kougeihinは個数で数えられる（工芸品と思われる）ものの番号．です．

次の原則，
ー　共通テスト「情報」最適化の原則　ー
ある変数の値がある変数に代入や比較されるならば単位はたぶん同じ．

から，[　コ　]が(4)なら，[　ケ　]は(1)，[　コ　]が(3)なら，[　ケ　]は(0)か(2)と思われます．

再び次の原則を適用すると

ー　共通テスト「情報」最適化の原則　ー
変数が連続代入されることはない

[　ケ　]は(0)でも(2)でもないことがわかります．(2)は行6で代入されていますし，(0)は行7で代入されています．つまりこれで[　コ　] は(4)，[　ケ　]は(1)の組み合わせであることがわかります．

次に[　サ　]，[　シ　]をみてみましょう．まず配列Nissuのインデクスに入りうるのはkougeihinでしょうか？tantouでしょうか？kougeihinは工芸品の番号で1-9, tantouは人の番号で1-3でした．Nissuの要素数は9でこれはkougeihinsuの9です．つまりは入るのはkougeihinと考えられます．また，tantouだとすると配列要素4-9の値は使われないことになってしまいます．そういう見方もありです．つまり次の2つの原則を使用します．

ー　共通テスト「情報」最適化の原則　ー
変数や配列の要素の値の単位が何になるか考えよ．

ー　共通テスト「情報」最適化の原則　ー
定義されている変数，配列が使われないことはない

すると[　サ　]，[　シ　]は(0),(2),(4)のいずれかだとわかります．10行目の表示関数の文字列　Akibi[tantou] , “日目〜”, Akibi[tantou] + [　サ　], “日目”　と期間を記載しています．期間ですので，例えば5日目から4日間の日数だと範囲としては5日目から(5+4-1)日目となります．つまり[　サ　]の解答は(2)であるとわかります．
10行目のAkibi[tantou] , “日目〜”　という表記から，どうもAkibi[tantou]は作業を開始する開始日であるとわかります．よって次の作業の開始日はおそらくAkibi[tantou]+Nissu[kougeihin]である．つまり[　シ　]の解答は(0)であると思われます．(4)のように配列要素のインデックスに-1が含まれる解が候補となるかは，次の原則

ー　共通テスト「情報」最適化の原則　ー
繰り返し文は1回目の繰り返しを考えて当てはめてみる．

を適用するとNissu[0]となってしまい，今回は1オリジンなので，これが不適であり，解の候補から外れることがわかります．
図4や図5とも完全なプログラムが分かれば，そこから逆に自然言語で書かれている説明文の空欄を埋めていくのは遥かに容易になります．

 

プログラムを実行されたい場合は 図5のプログラム をクリックしてください．

最後に

以上が，2025年度共通テスト「情報I」のプログラム問題の解説でした．一見テクニック集かと思われるかもしれませんが，いずれもデバッグやリファクタリングの際に行なっているプログラミングの自然な行為なのです．

 

 

 

高等学校情報科の授業利用を想定したネットワークシミュレータ「ピクトコルシミュレータ(Pictocol Simulator)」の使い方マニュアルをアップデートしました．

 

高等学校情報科の授業利用を想定したネットワークシミュレータ「ピクトコルシミュレータ(Pictocol Simulator)」の使い方マニュアルをアップデートしました．特徴として，コンピュータネットワークを学校生活の人間関係になぞらえて表示する機能や，共通テストでも出題の可能性があるトラブルシューティングの機能が挙げられます．

 

今回，情報科教員の先生方からのご要望でありました「アンカー文字列を直接アクセスして即座に特定のネットワーク構成が表示された状態での表示」や「ノード，リンクに対するラベル表示」などの機能に関する説明を追加しています．

 

ピクトグラミングWebサイト　https://pictogramming.org/ 　からアクセスください．

ピクトコルシミュレータ(Pictocol Simulator)に直接アクセスされたい場合は，こちらになります．

使いかたマニュアルにアクセスされたい場合は，こちらになります．

 

学会発表

1.前田祐杜,石井 幹大,伊藤 一成：人型ピクトグラムに着目した教育向けネットワークシュミレータ「Pictocol Simulator」の試作，第16回データ工学と情報マネジメントに関するフォーラム DEIM2024(2024.03)

2. 前田 祐杜,石井 幹大,伊藤 一成: ピクトグラムに着目した教育向けネットワークシミュレータ「Pictocol Simulator」の開発と評価, 情報処理学会研究報告 コンピュータと教育，CE177 (2024.12)

3.前田祐杜,石井 幹大,伊藤 一成：高等学校情報科の授業利用に特化した教育向けネットワークシミュレータの開発と評価，第17回データ工学と情報マネジメントに関するフォーラム DEIM2025(2025.03)

高等学校情報科の授業利用を想定したネットワークシミュレータ「ピクトコルシミュレータ(Pictocol Simulator)」をアップデートしました．

 

高等学校情報科の授業利用を想定したネットワークシミュレータ「ピクトコルシミュレータ(Pictocol Simulator)」をアップデートしました．特徴として，コンピュータネットワークを学校生活の人間関係になぞらえて表示する機能や，共通テストでも出題の可能性があるトラブルシューティングの機能が挙げられます．

 

今回，情報科教員の先生方からのご要望でありました「アンカー文字列を直接アクセスして即座に特定のネットワーク構成が表示された状態での表示」や「ノード，リンクに対するラベル表示」などの機能を追加しています．

 

ピクトグラミングWebサイト　https://pictogramming.org/ 　からアクセスください．

 

学会発表

1.前田祐杜,石井 幹大,伊藤 一成：人型ピクトグラムに着目した教育向けネットワークシュミレータ「Pictocol Simulator」の試作，第16回データ工学と情報マネジメントに関するフォーラム DEIM2024(2024.03)

2. 前田 祐杜,石井 幹大,伊藤 一成: ピクトグラムに着目した教育向けネットワークシミュレータ「Pictocol Simulator」の開発と評価, 情報処理学会研究報告 コンピュータと教育，CE177 (2024.12)

3.前田祐杜,石井 幹大,伊藤 一成：高等学校情報科の授業利用に特化した教育向けネットワークシミュレータの開発と評価，第17回データ工学と情報マネジメントに関するフォーラム DEIM2025(2025.03) 発表予定